Ejercicios
Solución:
Para poder solucionar este problema, basta con sustituir los valores arrojados en el mismo problema, por ejemplo tenemos el valor de la carga y también el valor de la fuerza que actúa sobre ese campo:
Ahora reemplazaremos estos datos en nuestra fórmula
Eso es lo que se generaría en la región donde actúa dicha fuerza sobre las cargas. Ahora veamos otro ejemplo con algunos incisos para entender por completo este tema.
Solución:
La imagen a la que se refiere el problema, es la que aparece justamente debajo.
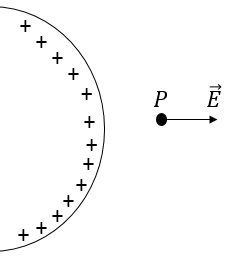 Para poder solucionar el problema, basta nuevamente en colocar nuestros datos en la fórmula.
Para poder solucionar el problema, basta nuevamente en colocar nuestros datos en la fórmula.
a) Al retirar la carga q y colocar en P una carga positiva de  ¿Cuál será el valor de la fuerza F que actuará sobre esa carga, y cuál es el sentido del movimiento que tenderá a adquirir?
¿Cuál será el valor de la fuerza F que actuará sobre esa carga, y cuál es el sentido del movimiento que tenderá a adquirir?
– Para poder solucionar esta parte, es necesario sustituir el nuevo valor de la carga en la fórmula … Perooo con la condición de que ahora la fuerza será la incógnita, es decir:
Hemos despejado F de la ecuación de campo eléctrico, entonces después de esto reemplazamos los datos.
Como la carga que hemos obtenido es positiva, entonces tenderá a moverse en el mismo sentido que el vector de E, es decir a la derecha. Para que podamos obtener un desplazamiento a la izquierda de E, entonces tendríamos que colocar una carga negativa.
Otro ejemplo que podemos encontrar es el siguiente.
Solución:
Para este sencillo problema, basta con reemplazar los datos en nuestra fórmula, pero antes de ello debemos despejarla en términos de q , de la siguiente forma.
Sustituyendo nuestros datos:
que con notación científica podemos dejarla expresada en 
que sería el valor de la carga a la que está sometida a un campo eléctrico y fuerza especificadas en el problema.
Veamos el último ejemplo empleando otra manera de la fórmula, como ya hemos visto en la explicación de la fórmula.
Solución:
En este problema se empleará la siguiente fórmula de campo eléctrico, pero haciendo uso de la distancia. Para ello colocamos los datos:
Sabemos que la fórmula es la siguiente:
Sustituyendo los datos en la fórmula:
Es decir que tenemos un campo eléctrico de la magnitud de 4.8×10^(4) N/C
Gracias por estas explicaciones, ha sido de mucha ayuda para mi aprendizaje.
ResponderEliminarSaludos
Muchasssss graciassssss 🙏
ResponderEliminarGracias 🫂
ResponderEliminarDe verdad muchas gracias
ResponderEliminar